B树与B+树
1 B树
在介绍B+树之前, 先简单的介绍一下B树,这两种数据结构既有相似之处,也有他们的区别,最后,我们也会对比一下这两种数据结构的区别。
1.1 B树概念
B树也称B-树,它是一颗多路平衡查找树。二叉树我想大家都不陌生,其实,B树和后面讲到的B+树也是从最简单的二叉树变换而来的,并没有什么神秘的地方,下面我们来看看B树的定义。
- 每个节点最多有m-1个 关键字 (可以存有的键值对)。
- 根节点最少可以只有1个 关键字 。
- 非根节点至少有m/2个 关键字 。
- 每个节点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
- 所有叶子节点都位于同一层,或者说根节点到每个叶子节点的长度都相同。
- 每个节点都存有索引和数据,也就是对应的key和value。
所以,根节点的 关键字 数量范围:1 <= k <= m-1,非根节点的 关键字 数量范围:m/2 <= k <= m-1。
另外,我们需要注意一个概念,描述一颗B树时需要指定它的阶数,阶数表示了一个节点最多有多少个孩子节点,一般用字母m表示阶数。
我们再举个例子来说明一下上面的概念,比如这里有一个5阶的B树,根节点数量范围:1 <= k <= 4,非根节点数量范围:2 <= k <= 4。
下面,我们通过一个插入的例子,讲解一下B树的插入过程,接着,再讲解一下删除关键字的过程。
1.2 B树插入
插入的时候,我们需要记住一个规则: 判断当前结点key的个数是否小于等于m-1,如果满足,直接插入即可,如果不满足,将节点的中间的key将这个节点分为左右两部分,中间的节点放到父节点中即可。
例子:在5阶B树中,结点最多有4个key,最少有2个key(注意:下面的节点统一用一个节点表示key和value)。
- 插入18,70,50,40

- 插入22

插入22时,发现这个节点的关键字已经大于4了,所以需要进行分裂,分裂的规则在上面已经讲了,分裂之后,如下。

- 接着插入23,25,39

分裂,得到下面的。

更过的插入的过程就不多介绍了,相信有这个例子你已经知道怎么进行插入操作了。
1.3 B树的删除操作
B树的删除操作相对于插入操作是相对复杂一些的,但是,你知道记住几种情况,一样可以很轻松的掌握的。
- 现在有一个初始状态是下面这样的B树,然后进行删除操作。

- 删除15,这种情况是删除叶子节点的元素,如果删除之后,节点数还是大于
m/2,这种情况只要直接删除即可。


- 接着,我们把22删除,这种情况的规则:22是非叶子节点, 对于非叶子节点的删除,我们需要用后继key(元素)覆盖要删除的key,然后在后继key所在的子支中删除该后继key 。对于删除22,需要将后继元素24移到被删除的22所在的节点。


此时发现26所在的节点只有一个元素,小于2个(m/2),这个节点不符合要求,这时候的规则(向兄弟节点借元素): 如果删除叶子节点,如果删除元素后元素个数少于(m/2),并且它的兄弟节点的元素大于(m/2),也就是说兄弟节点的元素比最少值m/2还多,将先将父节点的元素移到该节点,然后将兄弟节点的元素再移动到父节点 。这样就满足要求了。
我们看看操作过程就更加明白了。


- 接着删除28, 删除叶子节点 ,删除后不满足要求,所以,我们需要考虑向兄弟节点借元素,但是,兄弟节点也没有多的节点(2个),借不了,怎么办呢?如果遇到这种情况, 首先,还是将先将父节点的元素移到该节点,然后,将当前节点及它的兄弟节点中的key合并,形成一个新的节点 。

移动之后,跟兄弟节点合并。

删除就只有上面的几种情况,根据不同的情况进行删除即可。
上面的这些介绍,相信对于B树已经有一定的了解了,接下来的一部分,我们接着讲解B+树,我相信加上B+树的对比,就更加清晰明了了。
2 B+树
2.1 B+树概述
B+树其实和B树是非常相似的,我们首先看看 相同点 。
- 根节点至少一个元素
- 非根节点元素范围:m/2 <= k <= m-1
不同点 。
- B+树有两种类型的节点:内部结点(也称索引结点)和叶子结点。内部节点就是非叶子节点,内部节点不存储数据,只存储索引,数据都存储在叶子节点。
- 内部结点中的key都按照从小到大的顺序排列,对于内部结点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
- 每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
- 父节点存有右孩子的第一个元素的索引。
下面我们看一个B+树的例子,感受感受它吧!

2.2 插入操作
对于插入操作很简单,只需要记住一个技巧即可: 当节点元素数量大于m-1的时候,按中间元素分裂成左右两部分,中间元素分裂到父节点当做索引存储,但是,本身中间元素还是分裂右边这一部分的 。
下面以一颗5阶B+树的插入过程为例,5阶B+树的节点最少2个元素,最多4个元素。
- 插入5,10,15,20

- 插入25,此时元素数量大于4个了,分裂

- 接着插入26,30,继续分裂


有了这几个例子,相信插入操作没什么问题了,下面接着看看删除操作。
2.3 删除操作
对于删除操作是比B树简单一些的,因为 叶子节点有指针的存在,向兄弟节点借元素时,不需要通过父节点了,而是可以直接通过兄弟节移动即可(前提是兄弟节点的元素大于m/2),然后更新父节点的索引;如果兄弟节点的元素不大于m/2(兄弟节点也没有多余的元素),则将当前节点和兄弟节点合并,并且删除父节点中的key ,下面我们看看具体的实例。
- 初始状态
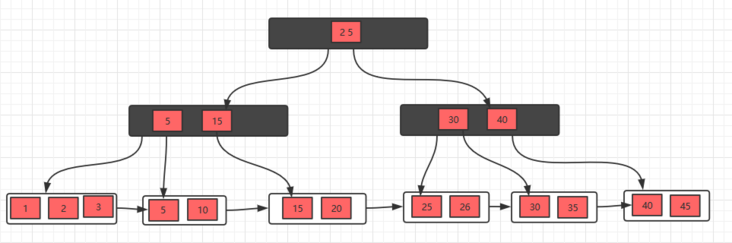
- 删除10,删除后,不满足要求,发现左边兄弟节点有多余的元素,所以去借元素,最后,修改父节点索引

- 删除元素5,发现不满足要求,并且发现左右兄弟节点都没有多余的元素,所以,可以选择和兄弟节点合并,最后修改父节点索引

- 发现父节点索引也不满足条件,所以,需要做跟上面一步一样的操作

这样,B+树的删除操作也就完成了,是不是看完之后,觉得非常简单!
3 B树和B+树总结
B+树相对于B树有一些自己的优势,可以归结为下面几点。
- 单一节点存储的元素更多,使得查询的IO次数更少,所以也就使得它更适合做为数据库MySQL的底层数据结构了。
- 所有的查询都要查找到叶子节点,查询性能是稳定的,而B树,每个节点都可以查找到数据,所以不稳定。
- 所有的叶子节点形成了一个有序链表,更加便于查找。
4 B树与B+树实现代码
B树实现代码
package com.btree;
import java.util.List;
public class BNode<K extends Comparable<K>, V> {
public List<K> keys;
public List<V> datas;
public BNode<K, V> parent;
public List<BNode<K, V>> children;
public BNode(List<K> keys, List<V> datas) {
this.keys = keys;
this.datas = datas;
}
public BNode(List<K> keys, List<V> datas, List<BNode<K, V>> children) {
this.keys = keys;
this.datas = datas;
this.children = children;
if (this.children != null) {
for (BNode<K, V> child : this.children) {
child.parent = this;
}
}
}
}
package com.btree;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/*
*
*
*
* 所有的新增操作一定发生在叶子节点,所有的叶子节点都位于同一层
*
*
* 新增:
* 分裂:
* 分裂一定从叶子节点开始
* 把分裂出来的俩个节点的后一个节点的第一个key上浮给父亲
* 需要注意孩子节点的分裂(针对非叶子节点)
*
* 删除:
* 叶子节点: 删除调整
*
*
*
* */
public class BTree<K extends Comparable<K>, V> {
public BNode<K, V> root;
private int degree;
private int upper;
private int under;
public int size;
public BTree(int degree) {
if (degree < 3) {
throw new IllegalArgumentException("BTree degree must > 2");
}
this.degree = degree;
this.upper = degree - 1;
this.under = (int) (Math.ceil((double) (degree / 2.0)) - 1);
this.size = 0;
this.root = new BNode<K, V>(toList(), toList(), null);
}
public void put(K key, V value) {
if (key == null) {
return;
}
BNode<K, V> cur = findDataNode(key);
int index = findEualKeyIndex(cur.keys, key);
if (index != -1) {
cur.datas.set(index, value);
return;
}
size++;
int ceilingKeyIndex = findCeilingKeyIndex(cur.keys, key);
cur.keys.add(ceilingKeyIndex, key);
cur.datas.add(ceilingKeyIndex, value);
split(cur);
}
public void split(BNode<K, V> cur) {
if (cur.keys.size() <= upper) {
return;
}
int midIndex = upper / 2;
List<K> allKeys = cur.keys;
List<V> allData = cur.datas;
List<BNode<K, V>> allChildren = cur.children;
List<BNode<K, V>> rightChildren = null;
List<BNode<K, V>> leftChildren = null;
if (cur.children != null && cur.children.size() > 0) {
leftChildren = new ArrayList<>(allChildren.subList(0, midIndex + 1));
rightChildren = new ArrayList<>(allChildren.subList(midIndex + 1, allChildren.size()));
}
List<K> leftKeys = new ArrayList<>(allKeys.subList(0, midIndex));
List<V> leftData = new ArrayList<>(allData.subList(0, midIndex));
List<K> rightKeys = new ArrayList<>(allKeys.subList(midIndex + 1, allKeys.size()));
List<V> rightData = new ArrayList<>(allData.subList(midIndex + 1, allData.size()));
BNode<K, V> left = new BNode<K, V>(leftKeys, leftData, leftChildren);
BNode<K, V> right = new BNode<K, V>(rightKeys, rightData, rightChildren);
if (cur == root) {
root = new BNode<K, V>(toList(allKeys.get(midIndex)), toList(allData.get(midIndex)), toList(left, right));
return;
}
BNode<K, V> parent = cur.parent;
int index = parent.children.indexOf(cur);
parent.children.remove(index);
parent.children.add(index, left);
parent.children.add(index + 1, right);
left.parent = parent;
right.parent = parent;
parent.keys.add(index, allKeys.get(midIndex));
parent.datas.add(index, allData.get(midIndex));
split(parent);
}
public void remove(K key) {
if (key == null || root == null || root.keys.size() == 0) {
return;
}
BNode<K, V> cur = findDataNode(key);
int index = findEualKeyIndex(cur.keys, key);
if (index == -1) {
return;
}
size--;
if (cur.children == null || cur.children.size() == 0) {
cur.keys.remove(index);
cur.datas.remove(index);
delete_maintain(cur);
return;
}
int ceilingKeyIndex = findCeilingKeyIndex(cur.keys, key);
int childIndex = findChildIndex(cur, ceilingKeyIndex, key);
BNode<K, V> successor = cur.children.get(childIndex);
while (successor.children != null && successor.children.size() > 0) {
successor = successor.children.get(0);
}
cur.keys.set(ceilingKeyIndex, successor.keys.remove(0));
cur.datas.set(ceilingKeyIndex, successor.datas.remove(0));
delete_maintain(successor);
}
public void delete_maintain(BNode<K, V> cur) {
if (cur.keys.size() >= under) {
return;
}
if (cur == root) {
if (cur.keys.size() == 0 && cur.children != null && cur.children.size() > 0) {
root = root.children.get(0);
return;
}
return;
}
int index = cur.parent.children.indexOf(cur);
BNode<K, V> leftBrother = index - 1 >= 0 ? cur.parent.children.get(index - 1) : null;
BNode<K, V> rightBrother = index + 1 < cur.parent.children.size() ? cur.parent.children.get(index + 1) : null;
if (leftBrother != null && leftBrother.keys.size() > under) {
// 向左兄弟借
// 该孩子先向父亲借
cur.keys.add(0, cur.parent.keys.get(index - 1));
cur.datas.add(0, cur.parent.datas.get(index - 1));
// 父亲再向左孩子借
cur.parent.keys.set(index - 1, leftBrother.keys.remove(leftBrother.keys.size() - 1));
cur.parent.datas.set(index - 1, leftBrother.datas.remove(leftBrother.datas.size() - 1));
// 如果该孩子节点非叶子节点,还要将左兄弟的最后一个孩子借过来
if (cur.children != null && cur.children.size() > 0) {
cur.children.add(0, leftBrother.children.remove(leftBrother.children.size() - 1));
cur.children.get(0).parent = cur;
}
} else if (rightBrother != null && rightBrother.keys.size() > under) {
// 向右兄弟借
// 该孩子先向父亲借
cur.keys.add(cur.parent.keys.get(index));
cur.datas.add(cur.parent.datas.get(index));
// 父亲再向右孩子借
cur.parent.keys.set(index, rightBrother.keys.remove(0));
cur.parent.datas.set(index, rightBrother.datas.remove(0));
// 如果该孩子是非叶子节点,还要将右兄弟的第一个孩子接过来
if (cur.children != null && cur.children.size() > 0) {
cur.children.add(rightBrother.children.remove(0));
cur.children.get(cur.children.size() - 1).parent = cur;
}
} else {
// 左兄弟或者右兄弟都没有,则需要将兄弟节点合并,合并是右兄弟节点合并到左兄弟节点上
if (leftBrother != null && leftBrother.keys.size() <= under) {
// 若该孩子节点的左兄弟存在,则将该节点合并到左兄弟上
// 先将父亲节点parentKeyIndex处的元素合并到左兄弟
leftBrother.keys.add(cur.parent.keys.remove(index - 1));
leftBrother.datas.add(cur.parent.datas.remove(index - 1));
// 再将当前节点的元素合并到左兄弟
leftBrother.keys.addAll(cur.keys);
leftBrother.datas.addAll(cur.datas);
// 若该节点是非叶子节点,则需要将该节点的孩子节点添加到左兄弟的孩子节点中
if (cur.children != null && cur.children.size() > 0) {
leftBrother.children.addAll(cur.children);
for (BNode<K, V> child : leftBrother.children) {
child.parent = leftBrother;
}
}
// 将该节点从父亲节点的孩子节点中移除
BNode<K, V> parent = cur.parent;
cur.parent.children.remove(index);
cur.keys = null;
cur.datas = null;
cur.parent = null;
cur.children = null;
cur = null;
delete_maintain(parent);
} else if (rightBrother != null && rightBrother.keys.size() <= under) {
// 若该节点的左兄弟不存在,则右兄弟一定存在
// 先将父亲节点parentKeyIndex处的元素合并到当前节点
cur.keys.add(cur.parent.keys.remove(index));
cur.datas.add(cur.parent.datas.remove(index));
// 再将右兄弟节点的元素合并到当前节点
cur.keys.addAll(rightBrother.keys);
cur.datas.addAll(rightBrother.datas);
// 若当前节点不是叶子节点,还需要将右兄弟节点的孩子节点合并过来
if (cur.children != null && cur.children.size() > 0) {
cur.children.addAll(rightBrother.children);
for (BNode child : cur.children) {
child.parent = cur;
}
}
// 将右兄弟节点从父亲节点的孩子节点中移除
BNode<K, V> parent = cur.parent;
cur.parent.children.remove(index + 1);
rightBrother.keys = null;
rightBrother.datas = null;
rightBrother.children = null;
rightBrother.datas = null;
rightBrother = null;
delete_maintain(parent);
}
}
}
public V get(K key) {
if (key == null || root == null) {
return null;
}
BNode<K, V> cur = findDataNode(key);
int index = findEualKeyIndex(cur.keys, key);
if (index == -1) {
return null;
}
return cur.datas.get(index);
}
public int findCeilingKeyIndex(List<K> keys, K key) {
int left = 0;
int right = keys.size() - 1;
int resIndex = keys.size();
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (key.compareTo(keys.get(mid)) <= 0) {
resIndex = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return resIndex;
}
public int findChildIndexByCeilingkeyIndex(List<K> keys, int ceilingKeyIndex, K key) {
if (ceilingKeyIndex == keys.size() || key.compareTo(keys.get(ceilingKeyIndex)) < 0) {
return ceilingKeyIndex;
}
return ceilingKeyIndex + 1;
}
public int findChildIndex(BNode<K, V> cur, int ceilingKeyIndex, K key) {
int childIndex = 0;
if (key.compareTo(cur.keys.get(0)) < 0) {
childIndex = 0;
} else if (key.compareTo(cur.keys.get(cur.keys.size() - 1)) > 0) {
childIndex = cur.children.size() - 1;
} else {
childIndex = findChildIndexByCeilingkeyIndex(cur.keys, ceilingKeyIndex, key);
}
return childIndex;
}
private BNode<K, V> findDataNode(K key) {
BNode<K, V> cur = root;
int ceilingKeyIndex = findCeilingKeyIndex(cur.keys, key);
int childIndex = findChildIndexByCeilingkeyIndex(cur.keys, ceilingKeyIndex, key);
if (ceilingKeyIndex < cur.keys.size() && key.compareTo(cur.keys.get(ceilingKeyIndex)) == 0) {
return cur;
}
while (cur.children != null && cur.children.size() > 0) {
cur = cur.children.get(childIndex);
ceilingKeyIndex = findCeilingKeyIndex(cur.keys, key);
childIndex = findChildIndexByCeilingkeyIndex(cur.keys, ceilingKeyIndex, key);
if (ceilingKeyIndex < cur.keys.size() && key.compareTo(cur.keys.get(ceilingKeyIndex)) == 0) {
return cur;
}
}
return cur;
}
private int findEualKeyIndex(List<K> keys, K key) {
int left = 0;
int right = keys.size() - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (key.compareTo(keys.get(mid)) == 0) {
return mid;
} else if (key.compareTo(keys.get(mid)) < 0) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
public <T> List<T> toList(T... t) {
ArrayList<T> ts = new ArrayList<>();
Collections.addAll(ts, t);
return ts;
}
}
package com.btree;
import java.util.*;
public class BTreeTest {
public static void main(String[] args) {
for (int i = 0; i < 100; i++) {
System.out.printf("第%d次测试\n", i);
int count = Test();
if (count != 10000000) {
break;
}
}
}
public static int Test() {
int degree = 3 + (int) (Math.random() * 200);
System.out.printf("degree:%d\n", degree);
TreeMap<Integer, Integer> treeMap = new TreeMap<>();
BTree<Integer, Integer> bTree = new BTree(degree);
System.out.println("start");
int times = 10000000;
int maxKey = 500;
int maxValue = 200;
int count = 0;
int getKey;
for (int i = 0; i < times; i++) {
count++;
int key = (int) (Math.random() * maxKey);
int value = (int) (Math.random() * maxValue);
if (Math.random() > 0.1) {
treeMap.put(key, value);
bTree.put(key, value);
}
int deleteKey = 0;
if (Math.random() < 0.2) {
deleteKey = (int) (Math.random() * maxKey);
treeMap.remove(deleteKey);
bTree.remove(deleteKey);
}
getKey = (int) (Math.random() * maxKey);
Integer treeMapGetKey = treeMap.get(getKey);
Integer bTreeGetKey = bTree.get(getKey);
if ((treeMapGetKey != null && bTreeGetKey == null) || (treeMapGetKey == null && bTreeGetKey != null)) {
System.out.println("get==> you are die!1 " + getKey + " " + treeMapGetKey + " " + bTreeGetKey);
break;
}
if ((treeMapGetKey != null && bTreeGetKey != null) && !treeMapGetKey.equals(bTreeGetKey)) {
System.out.println("get==> you are die!2 " + getKey + " " + treeMapGetKey + " " + bTreeGetKey);
break;
}
}
printAll(bTree.root);
System.out.println(count);
return count;
}
public static void printAll(BNode root) {
LinkedList<BNode> queue = new LinkedList<>();
queue.add(root);
StringBuilder sb = new StringBuilder();
int level = 1;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
BNode cur = queue.poll();
sb.append(cur.keys).append(" ");
if (cur.children != null && cur.children.size() > 0) {
queue.addAll(cur.children);
}
}
sb.append("\n");
sb.append("第" + (level++) + "层结束");
sb.append("\n");
}
System.out.println(sb.toString());
}
}
B+树实现代码
package com.bplustree;
import java.util.ArrayList;
import java.util.List;
public class BPlusNode<K extends Comparable<K>, V> {
//关键字
public List<K> keys;
//叶子节点数据项
public List<V> datas;
//非叶子节点 子节点
public List<BPlusNode<K, V>> children;
public BPlusNode<K, V> parent;
public BPlusNode<K, V> next;
public BPlusNode<K, V> pre;
public BPlusNode(List<K> keys, List<V> datas, List<BPlusNode<K, V>> children) {
this.keys = keys;
this.datas = datas;
this.children = children;
if (this.children != null) {
for (BPlusNode<K, V> child : children) {
child.parent = this;
}
}
}
}
package xp.bplustree;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class BPlusTree<K extends Comparable<K>, V> {
private int degree;
private int upper;
private int under;
public BPlusNode<K, V> root;
private BPlusNode<K, V> head;
private BPlusNode<K, V> tail;
private int size;
private int height;
public BPlusTree(int degree) {
if (degree < 3) {
throw new IllegalArgumentException("不支持度小于3的B+树");
}
this.degree = degree;
this.upper = degree - 1;
this.under = upper / 2;
this.root = new BPlusNode<K, V>(toList(), toList(), null);
this.head = root;
this.tail = root;
this.size = 0;
this.height = 1;
}
public void put(K key, V val) {
if (key == null) {
return;
}
BPlusNode<K, V> dataNode = findDataNode(key);
int index = findEqualKeyIndex(dataNode.keys, key);
if (index != -1) {
dataNode.data.set(index, val);
return;
}
size++;
int ceilKeyIndex = findCeilKeyIndex(dataNode.keys, key);
dataNode.keys.add(ceilKeyIndex, key);
dataNode.data.add(ceilKeyIndex, val);
data_node_split(dataNode);
}
public void data_node_split(BPlusNode<K, V> cur) {
if (cur.keys.size() <= upper) {
return;
}
int midIndex = upper / 2;
List<K> allKeys = cur.keys;
List<V> allData = cur.data;
List<K> leftKeys = new ArrayList<>(allKeys.subList(0, midIndex));
List<V> leftData = new ArrayList<>(allData.subList(0, midIndex));
List<K> rightKeys = new ArrayList<>(allKeys.subList(midIndex, allKeys.size()));
List<V> rightData = new ArrayList<>(allData.subList(midIndex, allData.size()));
BPlusNode<K, V> left = new BPlusNode<>(leftKeys, leftData, null);
BPlusNode<K, V> right = new BPlusNode<>(rightKeys, rightData, null);
if (cur.pre != null) {
cur.pre.next = left;
left.pre = cur.pre;
} else {
head = left;
left.pre = null;
}
if (cur.next != null) {
cur.next.pre = right;
right.next = cur.next;
} else {
tail = right;
right.next = null;
}
left.next = right;
right.pre = left;
if (cur == root) {
height++;
root = new BPlusNode<K, V>(toList(allKeys.get(midIndex)), null, toList(left, right));
return;
}
int index = cur.parent.children.indexOf(cur);
cur.parent.keys.add(index, allKeys.get(midIndex));
cur.parent.children.remove(index);
cur.parent.children.add(index, left);
cur.parent.children.add(index + 1, right);
left.parent = cur.parent;
right.parent = cur.parent;
BPlusNode<K, V> parent = cur.parent;
cur.pre = null;
cur.next = null;
cur.keys = null;
cur.data = null;
cur.parent = null;
index_node_split(parent);
}
private void index_node_split(BPlusNode<K, V> cur) {
if (cur.keys.size() <= upper) {
return;
}
int midIndex = upper / 2;
List<K> allKeys = cur.keys;
List<BPlusNode<K, V>> allChildren = cur.children;
List<K> leftKeys = new ArrayList<>(allKeys.subList(0, midIndex));
List<BPlusNode<K, V>> leftChildren = new ArrayList<>(allChildren.subList(0, midIndex + 1));
List<K> rightKeys = new ArrayList<>(allKeys.subList(midIndex + 1, allKeys.size()));
List<BPlusNode<K, V>> rightChildren = new ArrayList<>(allChildren.subList(midIndex + 1, allChildren.size()));
BPlusNode<K, V> left = new BPlusNode<>(leftKeys, null, leftChildren);
BPlusNode<K, V> right = new BPlusNode<>(rightKeys, null, rightChildren);
if (cur == root) {
height++;
root = new BPlusNode<K, V>(toList(allKeys.get(midIndex)), null, toList(left, right));
return;
}
int index = cur.parent.children.indexOf(cur);
cur.parent.keys.add(index, allKeys.get(midIndex));
cur.parent.children.remove(index);
cur.parent.children.add(index, left);
cur.parent.children.add(index + 1, right);
left.parent = cur.parent;
right.parent = cur.parent;
BPlusNode<K, V> parent = cur.parent;
cur.keys = null;
cur.data = null;
cur.children = null;
cur.parent = null;
index_node_split(parent);
}
public void remove(K key) {
if (key == null || root == null || root.keys == null || root.keys.size() == 0) {
return;
}
BPlusNode<K, V> dataNode = findDataNode(key);
int equalIndex = findEqualKeyIndex(dataNode.keys, key);
if (equalIndex == -1) {
return;
}
size--;
dataNode.keys.remove(equalIndex);
dataNode.data.remove(equalIndex);
data_node_delete_maintain(dataNode);
}
public void data_node_delete_maintain(BPlusNode<K, V> cur) {
if (cur.keys.size() >= under) {
return;
}
if (cur == root) {
return;
}
BPlusNode<K, V> leftBrother = cur.pre != null && cur.parent == cur.pre.parent ? cur.pre : null;
BPlusNode<K, V> rightBrother = cur.next != null && cur.parent == cur.next.parent ? cur.next : null;
BPlusNode<K, V> parent = cur.parent;
int index = parent.children.indexOf(cur);
if (leftBrother != null && leftBrother.keys.size() > under) {
cur.keys.add(0, leftBrother.keys.remove(leftBrother.keys.size() - 1));
cur.data.add(0, leftBrother.data.remove(leftBrother.data.size() - 1));
cur.parent.keys.set(index - 1, cur.keys.get(0));
} else if (rightBrother != null && rightBrother.keys.size() > under) {
cur.keys.add(rightBrother.keys.remove(0));
cur.data.add(rightBrother.data.remove(0));
cur.parent.keys.set(index, rightBrother.keys.get(0));
} else {
if (leftBrother != null && leftBrother.keys.size() <= under) {
cur.keys.addAll(0, leftBrother.keys);
cur.data.addAll(0, leftBrother.data);
cur.parent.keys.remove(index - 1);
cur.parent.children.remove(index - 1);
if (leftBrother.pre != null) {
leftBrother.pre.next = cur;
cur.pre = leftBrother.pre;
} else {
head = cur;
cur.pre = null;
}
leftBrother.pre = null;
leftBrother.next = null;
leftBrother.keys = null;
leftBrother.data = null;
leftBrother.parent = null;
index_node_delete_maintain(cur.parent);
} else if (rightBrother != null && rightBrother.keys.size() <= under) {
cur.keys.addAll(rightBrother.keys);
cur.data.addAll(rightBrother.data);
cur.parent.keys.remove(index);
cur.parent.children.remove(index + 1);
if (rightBrother.next != null) {
rightBrother.next.pre = cur;
cur.next = rightBrother.next;
} else {
tail = cur;
cur.next = null;
}
rightBrother.pre = null;
rightBrother.next = null;
rightBrother.keys = null;
rightBrother.data = null;
rightBrother.parent = null;
index_node_delete_maintain(cur.parent);
}
}
}
private void index_node_delete_maintain(BPlusNode<K, V> cur) {
if (cur.keys.size() >= under) {
return;
}
if (cur == root) {
if (cur.keys.size() == 0) {
height--;
root = cur.children.get(0);
}
return;
}
BPlusNode<K, V> parent = cur.parent;
int index = parent.children.indexOf(cur);
BPlusNode<K, V> leftBrother = index - 1 >= 0 ? parent.children.get(index - 1) : null;
BPlusNode<K, V> rightBrother = index + 1 < parent.children.size() ? parent.children.get(index + 1) : null;
if (leftBrother != null && leftBrother.keys.size() > under) {
cur.keys.add(0, cur.parent.keys.remove(index - 1));
cur.parent.keys.add(index - 1, leftBrother.keys.remove(leftBrother.keys.size() - 1));
cur.children.add(0, leftBrother.children.remove(leftBrother.children.size() - 1));
cur.children.get(0).parent = cur;
} else if (rightBrother != null && rightBrother.keys.size() > under) {
cur.keys.add(parent.keys.remove(index));
parent.keys.add(index, rightBrother.keys.remove(0));
cur.children.add(rightBrother.children.remove(0));
cur.children.get(cur.children.size() - 1).parent = cur;
} else {
if (leftBrother != null && leftBrother.keys.size() <= under) {
cur.keys.add(0, cur.parent.keys.remove(index - 1));
cur.keys.addAll(0, leftBrother.keys);
cur.children.addAll(0, leftBrother.children);
for (BPlusNode<K, V> child : leftBrother.children) {
child.parent = cur;
}
cur.parent.children.remove(index - 1);
leftBrother.keys = null;
leftBrother.data = null;
leftBrother.children = null;
leftBrother.parent = null;
index_node_delete_maintain(cur.parent);
} else if (rightBrother != null && rightBrother.keys.size() <= under) {
cur.keys.add(cur.parent.keys.remove(0));
cur.keys.addAll(rightBrother.keys);
cur.children.addAll(rightBrother.children);
for (BPlusNode<K, V> child : rightBrother.children) {
child.parent = cur;
}
cur.parent.children.remove(index + 1);
rightBrother.keys = null;
rightBrother.data = null;
rightBrother.children = null;
rightBrother.parent = null;
index_node_delete_maintain(cur.parent);
}
}
}
public V get(K key) {
if (key == null || root == null || root.keys == null || root.keys.size() == 0) {
return null;
}
BPlusNode<K, V> dataNode = findDataNode(key);
int equalIndex = findEqualKeyIndex(dataNode.keys, key);
return equalIndex == -1 ? null : dataNode.data.get(equalIndex);
}
public boolean containsKey(K key) {
return get(key) != null;
}
public K firstKey() {
return head.keys == null ? null : head.keys.get(0);
}
public K lastKey() {
return tail.keys == null ? null : tail.keys.get(tail.keys.size() - 1);
}
public int size() {
return size;
}
public int height() {
return height;
}
private BPlusNode<K, V> findDataNode(K key) {
BPlusNode<K, V> cur = root;
while (cur.children != null && cur.children.size() > 0) {
int ceilKeyIndex = findCeilKeyIndex(cur.keys, key);
int childIndex = findChildIndex(cur.keys, ceilKeyIndex, key);
cur = cur.children.get(childIndex);
}
return cur;
}
private int findChildIndex(List<K> keys, int ceilKeyIndex, K key) {
if (ceilKeyIndex == keys.size() || key.compareTo(keys.get(ceilKeyIndex)) < 0) {
return ceilKeyIndex;
}
return ceilKeyIndex + 1;
}
private int findEqualKeyIndex(List<K> keys, K key) {
int left = 0;
int right = keys.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (key.compareTo(keys.get(mid)) == 0) {
return mid;
} else if (key.compareTo(keys.get(mid)) < 0) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
private int findCeilKeyIndex(List<K> keys, K key) {
int left = 0;
int right = keys.size() - 1;
int res = keys.size();
while (left <= right) {
int mid = left + (right - left) / 2;
if (key.compareTo(keys.get(mid)) <= 0) {
res = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return res;
}
public <T> List<T> toList(T... t) {
List<T> list = new ArrayList<>();
Collections.addAll(list, t);
return list;
}
}
package com.bplustree;
import java.util.LinkedList;
import java.util.NoSuchElementException;
import java.util.TreeMap;
public class BPlusTreeTest {
public static void main(String[] args) {
for (int i = 0; i < 100; i++) {
System.out.printf("第%d次测试\n", i);
int count = Test();
if (count != 10000000) {
break;
}
}
}
public static int Test() {
int degree = 3 + (int) (Math.random() * 200);
System.out.printf("degree:%d\n", degree);
TreeMap<Integer, Integer> treeMap = new TreeMap<>();
BPlusTree<Integer, Integer> sbTree = new BPlusTree<Integer, Integer>(degree);
System.out.println("start");
int times = 10000000;
int maxKey = 500;
int maxValue = 1000000;
int count = 0;
int getKey = 0;
for (int i = 0; i < times; i++) {
count++;
int key = (int) (Math.random() * maxKey);
int value = (int) (Math.random() * maxValue);
if (Math.random() > 0.1) {
treeMap.put(key, value);
sbTree.put(key, value);
}
int deleteKey = 0;
if (Math.random() < 0.5) {
deleteKey = (int) (Math.random() * maxKey);
treeMap.remove(deleteKey);
sbTree.remove(deleteKey);
}
getKey = (int) (Math.random() * maxKey);
Integer treeMapGetkey = treeMap.get(getKey);
Integer avlGetkey = sbTree.get(getKey);
if ((treeMapGetkey != null && avlGetkey == null) || (treeMapGetkey == null && avlGetkey != null)) {
System.out.println("get==> you are die!1 " + getKey + " " + treeMapGetkey + " " + avlGetkey + " delete:" + deleteKey);
break;
}
if (treeMapGetkey != null && avlGetkey != null && !treeMapGetkey.equals(avlGetkey)) {
System.out.println("get==> you are die!2 " + getKey + " " + treeMapGetkey + " " + avlGetkey);
break;
}
int containsKey = (int) (Math.random() * maxKey);
if (treeMap.containsKey(containsKey) != sbTree.containsKey(containsKey)) {
System.out.println("containsKey==> you are die!");
break;
}
Integer treeMapFirstKey = null;
Integer avlFirstKey = null;
try {
treeMapFirstKey = treeMap.firstKey();
avlFirstKey = sbTree.firstKey();
} catch (NoSuchElementException e) {
}
if ((treeMapFirstKey != null && avlFirstKey == null) || (treeMapFirstKey == null && avlFirstKey != null)) {
System.out.println("firstKey==> you are die! " + " " + treeMapFirstKey + " " + avlFirstKey);
break;
}
if ((treeMapFirstKey != null && avlFirstKey == null) || (treeMapFirstKey == null && avlFirstKey != null)) {
System.out.println("firstKey==> you are die! " + " " + treeMapFirstKey + " " + avlFirstKey);
break;
}
if (treeMapFirstKey != null && avlFirstKey != null && !treeMapFirstKey.equals(avlFirstKey)) {
System.out.println("firstKey==> you are die!" + " " + treeMapFirstKey + " " + avlFirstKey);
break;
}
Integer treeMapLastKey = null;
Integer avlLastKey = null;
try {
treeMapLastKey = treeMap.lastKey();
avlLastKey = sbTree.lastKey();
} catch (NoSuchElementException e) {
}
if ((treeMapLastKey != null && avlLastKey == null) || (treeMapLastKey == null && avlLastKey != null)) {
System.out.println("lastKey==> you are die! " + " " + treeMapLastKey + " " + avlLastKey);
break;
}
if (treeMapLastKey != null && avlLastKey != null && !treeMapLastKey.equals(avlLastKey)) {
System.out.println("lastKey==> you are die!" + " " + treeMapLastKey + " " + avlLastKey);
break;
}
if (treeMap.size() != sbTree.size()) {
System.out.println("size==> you are die!" + treeMap.size() + " " + sbTree.size());
break;
}
}
System.out.println("B+树的高度为:" + sbTree.height());
printAll(sbTree.root);
System.out.println("end " + count);
return count;
}
public static void printAll(BPlusNode<Integer, Integer> root) {
LinkedList<BPlusNode<Integer, Integer>> queue = new LinkedList<>();
queue.add(root);
StringBuilder res = new StringBuilder();
int level = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; ++i) {
BPlusNode<Integer, Integer> cur = queue.poll();
res.append(cur.keys).append(" ");
if (cur.children != null && cur.children.size() > 0) {
queue.addAll(cur.children);
}
}
res.append("\n");
res.append("第" + (++level) + " 层结束");
res.append("\n");
}
System.out.println(res.toString());
}
}